Cube and Cuboid in hindi अर्थ घन तथा घनाभ होता है। रीजनिंग में Cube and Cuboid से कई सवाल पूछे जाते है। अच्छे अंक लाने की दृष्टि से रीजनिंग में पूछे जाने वाले Cube and Cuboid Questions and Answers को विस्तार से समझाया गया है। प्रश्नों से सम्बंधित परेशानी को दूर करने के लिए cube and cuboid images को भी लेख में दिया गया है।
घन तथा घनाभ से Railway, SSC, Banking, Police तथा अन्य कई प्रतियोगी परीक्षाओं में प्रश्न पूछे जाते है। परीक्षा में अधिक अंक लाने के लिए इस पाठ की तैयारी अति आवश्यक है।
रीजनिंग में घन तथा घनाभ से सतह पर रंगे फलकों से जुड़े सवाल पूछे जाते है। Reasoning में Cube and Cuboid Formula and Tricks की सहायता से सवालों को तेजी से हल कर सकते है। सवालों की प्रैक्टिस के लिए कई सारे cube and cuboid questions and answers को भी समझाया गया है।
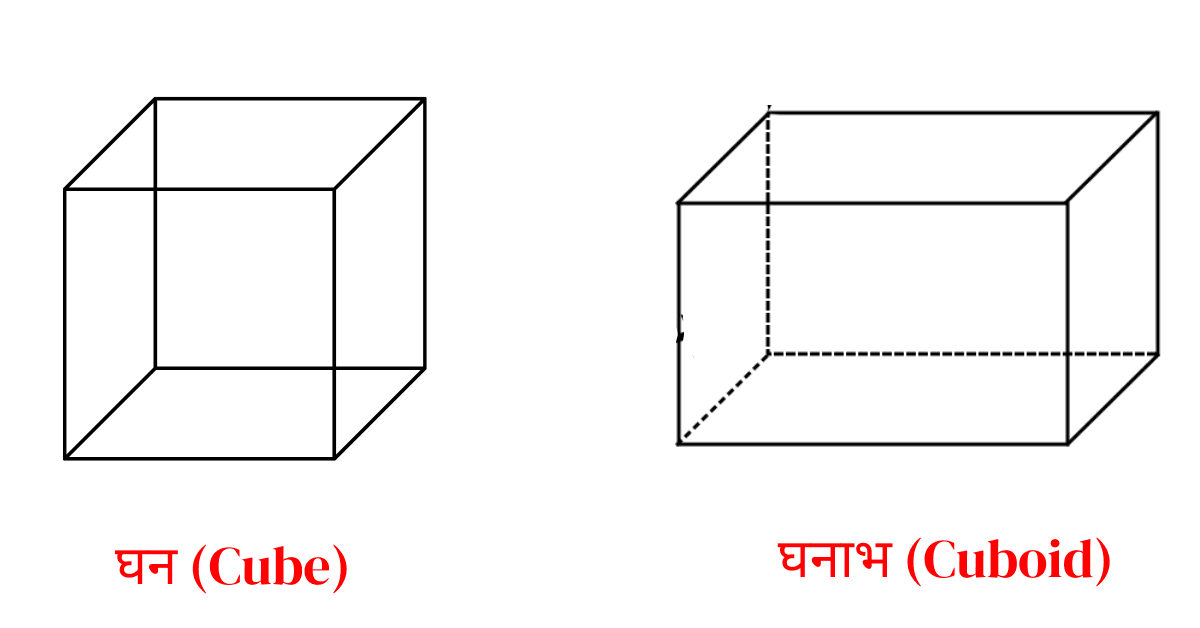
घन परिभाषा | Cube Definition
छः वर्गाकार फलकों से बनी आकृति को घन (Cube) है। यही घन की परिभाषा भी है।
घन में लम्बाई, चौड़ाई, ऊँचाई तीनों होती है। इसीलिए घन एक त्रिविमीय आकृति होती है। उदाहरण- रुबिक क्यूब, लूडो का पासा, समान लम्बाई चौड़ाई ऊंचाई की वस्तु भी घन कहलाती है।
| घन की विशेषता | संख्या |
|---|---|
| फलक (सतह) Surface | 6 |
| भुजा (Side) | 12 |
| शीर्ष (Edge) | 8 |
| विकर्ण (Diagonal) | 4 |
घन की सभी भुजा समान लम्बाई की होती है। घन के विकर्ण भी समान लम्बाई के होते है।
घन तथा घनाभ से सम्बंधित रीजनिंग के सवाल को हल करने के लिए घन की इतनी जानकारी काफी है। रीजनिंग में घन से इस प्रकार प्रश्न पूछे जाते है कि-
एक 10 सेमी के घन को 2 सेमी के छोटे भागों में बांटा गया है तो ऐसे कितने छोटे घन होंगे जिनके 3 सतह रंगी हो, जिनकी 2 सतह रंगी हो, जिनकी 1 सतह रंगी हो तथा ऐसे कितने घन होंगे जिनकी एक भी सतह रंगी न हो?
अब हम प्रश्न की सहायता से घन तथा घनाभ के रीजनिंग सम्बन्धी सवालों को हल करने के फॉर्मूला और ट्रिक को समझेंगे।
यदि पासा (Dice) सम्बंधित रीजनिंग प्रश्नों को हल करने का तरीका जानना चाहते है तो-
Cube and Cuboid Questions Trick in Reasoning
प्रश्न- एक 6cm के घन को 2 सेमी के छोटे भागों में बांटा गया है तो ऐसे कितने छोटे घन होंगे-
1.) जिनके 3 सतह रंगी हो
2.) जिनकी 2 सतह रंगी हो
3.) जिनकी 1 सतह रंगी हो
4.)जिनकी एक भी सतह रंगी न हो?
उत्तर-
n= बड़े घन की भुजा ÷ छोटे घन की भुजा
n= 6 ÷ 2
n= 3
1.) छोटे घन जिनकी 3 सतह रंगी हो = 8 (प्रत्येक स्थिति में 3 सतह पर रंगे घन 8 ही होंगे)
2.) छोटे घन जिनकी दो सतह रंगी हो सूत्र = 12 (n-2)
=12 (3-2)
= 12
3.) छोटे घन जिनकी एक सतह रंगी हो सूत्र = 6 (n-2)²
= 6 (3-2)²
= 6 × 1²
= 6
4.) छोटे घन जिनकी एक भी सतह न रंगी हो सूत्र = (n-2)³
= (3-2)³
=1³
=1
इस प्रकार हम रीजनिंग में भिन्न-भिन्न सतह पर रंगे घन की संख्या को निकल सकते है। नीचे दिए गए टेबल की सहायता से Formula को याद कर ले।
Cube and Cuboid Formula in hindi
| क्रम सं | पूछने का प्रकार | फार्मूला (Formula) |
|---|---|---|
| 1. | जब 3 सतह रंगी हो | 8 |
| 2. | जब 2 सतह रंगी हो | 12 (n-2) |
| 3. | जब 1 सतह रंगी हो | 6 (n-2)² |
| 4. | जिनकी कोई सतह न रंगी हो | (n-2)³ |
यहा n = बड़े घन की भुजा ÷ छोटे घन की भुजा है।
अतः कुल फार्मूला=
Formula 1.) $$\mathbf n\boldsymbol=\frac{\mathbf{Big}\boldsymbol\;\mathbf{Cube}\boldsymbol\;\mathbf{Side}}{\mathbf{Small}\boldsymbol\;\mathbf{Cube}\boldsymbol\;\mathbf{Side}}$$
Formula 2.) $$\mathbf{No}\boldsymbol.\boldsymbol\;\mathbf{of}\boldsymbol\;\mathbf{small}\boldsymbol\;\mathbf{Cube}\boldsymbol=\mathbf{\left(\frac{\mathrm{Big}\;\mathrm{Cube}\;\mathrm{Side}}{\mathrm{Small}\;\mathrm{Cube}\;\mathrm{Side}}\right)}^{\mathbf3}$$
Formula 3.) Number of Small Cubes= (n)³
Cube and Cuboid Questions and Answers
Question 1.) एक 12 cm के घन को 3 cm के छोटे घन में काटा जाता है तो कुल कितने घन बनेंगे?
छोटे घन की संख्या= (बड़े घन की भुजा ÷ छोटे घन की भुजा)³
Number of small Cubes= (Big cube side ÷ small Cube side)³
छोटे घन की संख्या= (12 ÷ 3)³
=4³
=64
अतः कुल 64 छोटे घन बनेंगे।
Question 2.) एक रंगीन घन को कुल 216 छोटे-छोटे घन में काटा जाता है तो कुल कितने रंगहीन घन बनेंगे?
Formula 3 से छोटे घन की संख्या = (n)³
216 = (n)³
3√216 = n
n = 6
ऊपर टेबल में दिए सूत्र से हम जानते है कि-
रंगहीन घन या घन जिनकी कोई सतह न रंगी हो = (n-2)³
= (6 – 2)³
उत्तर = 64 रंगहीन घन प्राप्त होंगे।
Question 3.) एक रंगीन घन को 125 छोटे घन में बांटा गया है तो ऐसे कितने घन होंगे जिनकी कम से कम 2 सतह रंगीन हो?
Note: यंहा कम से कम 2 सतह से अर्थ निकलता है कि= 2 सतह पर रंगीन घन + 3 सतह पर रंगीन घन
छोटे घन की संख्या = (n)³
125 = (n)³
n = 5
2 सतह पर रंगीन घन = 12 (n-2)
= 12 (5-2)
=36
3 सतह पर रंगीन घन = 8
कम से कम 2 सतह पर रंगीन घन = 36 + 8
उत्तर कम से कम 2 सतह पर रंगीन घन = 44 छोटे घन
Question 4.) एक रंगीन घन को 216 छोटे घन में बांटा गया है तो ऐसे कितने घन होंगे जिनकी कम से कम 1 सतह रंगीन हो?
Note: यंहा कम से कम से 1 सतह से अर्थ निकलता है कि= 1 सतह पर रंगीन घन + 2 सतह पर रंगीन घन + 3 सतह पर रंगीन घन
छोटे घन की संख्या = (n)³
216 = (n)³
n = 6
1 सतह पर रंगीन घन = 6 (n-2)²
= 6 (6-2)²
=96
2 सतह पर रंगीन घन = 12 (n-2)
= 12 (6-2)
= 48
3 सतह पर रंगीन घन = 8
कम से कम 1 सतह पर रंगीन घन = 96 + 48 + 8
कम से कम 1 सतह पर रंगीन घन = 152
इन सूत्रों तथा ट्रिक का इस्तेमाल करके आप घन तथा घनाभ के प्रश्नों को हल कर सकते है। रीजनिंग के अन्य टॉपिक की प्रैक्टिस के लिए किताब से तैयारी कर सकते है।
Join us now
प्रश्नों को हल करने में अन्य किसी जानकारी के लिए कमेंट बॉक्स में कमेंट करे।
- International Men’s Day 2024: इंटरनेशनल मेन्स डे कब मनाया जाता है?, क्या होता है? क्यों मनाया जाता है?, इंटरनेशनल मेन्स डे 2024 थीम, कैसे मनाया जाता है?, महत्व जानें
- इंजीनियरिंग ड्राइंग में रेखाएं कितने प्रकार की होती है?, इंजीनियरिंग ड्राइंग में रेखा किसे कहते है?, विभिन्न रेखाओं के उपयोग, विशेषता, मोटाई, उदाहरण चित्र सहित जानें
- Ibps rrb po mains result 2024 कैसे चेक करें? इंटरव्यू कितने अंक का होता है? महत्वपूर्ण जानकारी
- इंजीनियरिंग ड्राइंग में टाइटल ब्लॉक को कैसे बनाते हैं?, टाइटल ब्लॉक का डिज़ाइन, आकार, प्रकार, परिभाषा, 8 जरुरी सावधानियों को जानें
- न्यूटन का पहला नियम (Newton’s First Law): परिभाषा, कारण, अनुप्रयोग, उदाहरण | जड़त्व का नियम (Law of Inertia), प्रकार
- Engineering (13)
- Exam Info (9)
- Mathematics (5)
- Physics (22)
- Reasoning (15)