भौतिक विज्ञान में अभिकेंद्र त्वरण एक महत्वपूर्ण टॉपिक है। अभिकेंद्र त्वरण वृत्तीय गति पाठ के अंतर्गत आता है। अभिकेंद्र त्वरण समझने के बाद ही हम अभिकेंद्र बल को अच्छे ढंग से समझ सकते है। जब कोई कण वृत्तीय पथ पर गति करता है तो पथ के केंद्र की ओर कार्य करने वाले त्वरण को अभिकेंद्र त्वरण कहते है।
इस लेख में हम अभिकेंद्र त्वरण किसे कहते है, परिभाषा, मात्रक, विमीय सूत्र, अभिकेंद्र त्वरण का सूत्र तथा अभिकेंद्र त्वरण के सूत्र का निगमन भी बेहतरीन तरीके से स्थापित करेंगे।
अभिकेंद्र त्वरण किसे कहते है? | अभिकेंद्र त्वरण की परिभाषा
जब कोई कण एकसमान चाल से वृत्तीय पथ पर गति कर रहा है तो कण की दिशा लगातार बदलती जाती है अर्थात वेग लगातार बदलता जाता है। इस स्थिति में कण की वेग की दिशा के लंबवत तथा वृत्त के केंद्र की ओर एक त्वरण कार्य करता है, इस त्वरण को अभिकेंद्र त्वरण कहते है। यही अभिकेंद्र त्वरण की परिभाषा है।
अभिकेंद्र त्वरण को α से प्रदर्शित करते है। अभिकेंद्र त्वरण की दिशा सदैव वृत्त के केंद्र की ओर रहती है।
नोट: अभिकेंद्र त्वरण में कण का वेग नहीं बदलता है लेकिन दिशा लगातार बदलती रहती है।
मात्रक- अभिकेंद्र त्वरण का मात्रक मीटर/सेकण्ड² होता है।
विमीय सूत्र- अभिकेंद्र त्वरण का विमीय सूत्र L T-2 होता है।
अभिकेंद्र त्वरण का सूत्र | अभिकेंद्र त्वरण का व्यंजक
अभिकेंद्र त्वरण के सूत्र का व्यंजक-
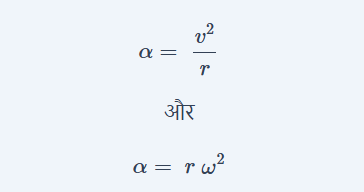
ये दोनों सूत्र ही अभिकेंद्र त्वरण के है। इस सूत्र में-
- α= अभिकेंद्र त्वरण
- v= रेखीय वेग
- r= वृत्तीय पथ की त्रिज्या
- ω= कोणीय वेग
अभिकेंद्र त्वरण का सूत्र का व्युत्पन्न | Centripetal Acceleration Formula Proving
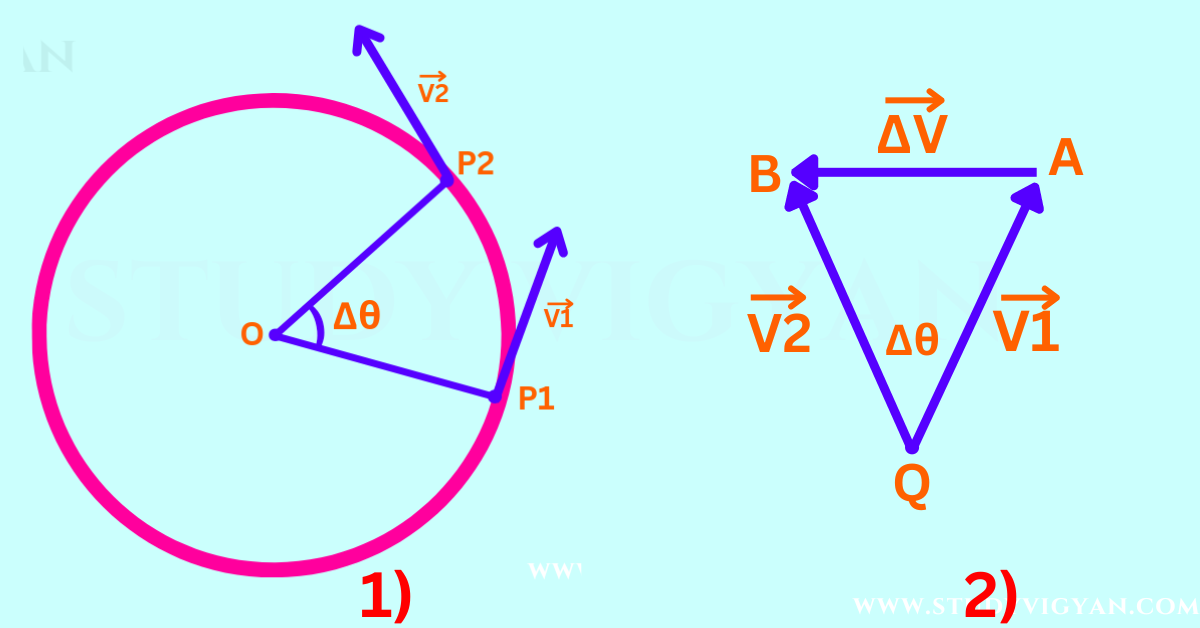
माना कोई कण वृत्तीय पथ पर एक समान चाल से चल रहा है। इस वृतीय पथ का केंद्र O तथा त्रिज्या r है। वृतीय पथ के सभी बिंदु पर कण के वेग की दिशा वृत्तीय पथ के स्पर्शरेखीय (Tangential) होती है।
माना वह कण बहुत थोड़े समयान्तराल ∆t में बिन्दु P1 से बिंदु P2 तक ∆s दूरी तय करता है।
इन बिंदु पर कण का वेग क्रमशः वेक्टर v1 तथा v2 है। वेग वेक्टर v1 तथा v2 दोनों के परिमाण v है लेकिन इनकी दिशाओं में ∆θ कोण का अंतर है।
बिंदु P1 से P2 तक वेग परिवर्तन (∆v)=
(∆v) = vector v2– vector v1
यदि हम वेक्टर v1 व v2 को एक ही बिंदु Q से खींचे तथा एक तीसरे सदिश ∆v द्वारा वेक्टर v1 के तीर वाले हिस्से को वेक्टर v2 के तीर वाले हिस्से से मिलाये तो तीसरा सदिश ∆v वेग-परिवर्तन को व्यक्त करेगा अतः (∆v) = vector v2– vector v1
इससे पता चलता है कि त्रिभुज OP1P2 तथा वेक्टर त्रिभुज QAB समरूप है। (प्रत्येक त्रिभुज की दो भुजायें बराबर है तथा इनके बीच का कोण ∆θ है। अतः इन दोनों त्रिभुजों में-

यह मान समीकरण (1) में रखने पर-

कोणीय वेग (Angular Velocity) के पद में यही अभिकेंद्र त्वरण (Centripetal Acceleration) का सूत्र है।

अभिकेंद्रीय त्वरण के उदाहरण | Centripetal Acceleration Examples
- कार जब सड़क में मोड़ पर मुड़ती है तो कार पर वृत्तीय पथ के केंद्र की ओर अभिकेंद्र त्वरण कार्य करता है।
- नगण्य भार के कण को डोरी से बांधकर वृत्तीय पथ पर घुमाने पर अभिकेंद्र त्वरण लगता है।
- परमाणु में नाभिक के चारों ओर घूम रहे इलेक्ट्रॉन पर भी त्वरण कार्य करता है।
- पृथ्वी का सूर्य के चारों ओर घूमना पर भी अभिकेंद्र त्वरण कार्य करता है।
FAQ (Frequently Asked Questions)
अभिकेंद्रीय त्वरण व्युत्पन्न कैसे होता है?
अभिकेंद्रीय त्वरण का व्युत्पन्न वृत्तीय पथ पर गति कर रहे कण की दिशा को वेक्टर सहायता से दो त्रिभुजों में समरूपता स्थापित करके अभिकेंद्र त्वरण का व्युत्पन्न किया जाता है। लेख में व्युत्पन्न पूरा करके आसान भाषा में समझाया गया है।