Power, Indices and Surds Formula, Questions, Rules, Meaning in Hindi

Share with friends

गणित के Power, Indices and Surds पाठ से प्रतियोगी परीक्षाओं में कई सारे सवाल पूछे जाते है। इसलिए Power, Indices and Surds Formula, Questions, Rules, Meaning in Hindi को अच्छी तरह से पढ़ना आवश्यक है।

Power, Indices and Surds in hindi में घात, घातांक और करणी कहते है। इसका उपयोग गणित के अलग-अलग सवाल जैसे बीजगणित, अंकगणित आदि में होता रहता है।

Table of Contents

Power, Indices and Surds Formula

Power, Indices and Surds Questions को हल करने के लिए कई सारे Formula की जरुरत पड़ती है। इन सभी फॉर्मूलों को एक साथ मिलने मुश्किल होता है। नीचे सभी Surds, Indices Formula को table में बेहतरीन तरीके से दिया गया है। सभी 14 Power, Indices and Surds Formula को एक साथ दिया गया है।

इन फॉर्मूलों को याद कर ले। इनकी सहायता से ही प्रश्नों को हल किया जाता है। एक तौर पर इन फॉर्मूलों को Power, Indices and Surds Rules भी कहा जा सकता है।

S. No.	Power, Indices and Surds Formula
Formula No. 1	$$ a^m \cdot a^n = a^{m+n} $$
Formula No. 2	$$ \frac{a^m}{a^n} = a^{m-n}, \quad (a \ne 0) $$
Formula No. 3	$$ (a^m)^n = a^{mn} $$
Formula No. 4	$$ (ab)^n = a^n \cdot b^n $$
Formula No.5	$$ \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} $$
Formula No. 6	$$ a^0 = 1, \quad (a \ne 0) $$
Formula No. 7	$$ a^{-n} = \frac{1}{a^n} $$
Formula No. 8	$$ \sqrt[n]{a} = a^{1/n} $$
Formula No. 9	$$ \sqrt{a} = a^{1/2} $$
Formula No. 10	$$ a^{m/n} = \sqrt[n]{a^m} $$
Formula No. 11	$$ \sqrt{a} \times \sqrt{b} = \sqrt{ab} $$
Formula No. 12	$$\left(\frac{a}{b}\right)^n = \left(\frac{b}{a}\right)^{-n} $$
Formula No. 13	$$ (a^p)^q = a^{p \times q} = a^{q \times p} = (a^q)^p $$
Formula No. 14	aⁿ = a × a × a × a × a × a ….. n times

Power, Indices and Surds Rules

घातांक एवं करणी के सवालों को हल करने के लिए Power, Indices and Surds Rules की भी जरुरत पड़ती है। इन नियम के द्वारा सवालों को छोटे रूप में बाँटकर उत्तर ज्ञात किया जाता है। इसके 2 मुख्य नियम (Power indices rules) है जो निम्न प्रकार है:

Rule No. 1 समान आधार होने पर नियम (Same Base Rule)

Power, Indices and Surds के इस नियम के अनुसार, अगर नीचे के पद समान है तो बराबर के दाएं और बाएं ओर स्थित घात (Power) समान होती है।

अगर a^m = aⁿ हो तो-

m = n

उदाहरण: अगर za = z⁷ है तो,

a = 7 होता है।

Exception: 1⁵ = 1⁶ हो तो
5, 6 के बराबर नहीं हो सकता है। अतः 1 की घात दोनों होने पर यह नही लागू होता है।

0³ = 0⁵ हो तो
3, 5 के बराबर नहीं हो सकता है। अतः 0 की घात दोनों होने पर यह नही लागू होता है।

Rule No. 2 समान घात होने पर नियम (Same Power Rule)

Power, Indices and Surds के इस नियम के अनुसार, अगर बराबर के दाएं और बाएं ओर स्थित घात समान है तो निचले पद भी आपस में समान होते है।

अगर a^m = b^m हो तो-

a = b

उदाहरण: अगर z² = 4² है तो,

z = 2 होता है।

घात की परिभाषा (Power or Exponents Definition)

किसी संख्या को खुद से कितनी बार गुणा किया गया है इसे दर्शाने के लिए घात रूप का इस्तेमाल किया जाता है। यही घात की परिभाषा (Power or Exponents Definition) भी है।

मुख्य रूप (Main Form): aⁿ = a × a × a × a × a…. n times

a = आधार (Base)
n = घातांक (Exponent या Index)
aⁿ = a को n बार गुणा करना

उदाहरण (Surds and Indices Examples):

2⁴ = 2 × 2 × 2 × 2 = 16
3⁵ = 3 × 3 × 3 × 3 ×3 = 243

करणी की परिभाषा (Surds Definition)

वह अपरिमेय संख्या जिसका मूल (वर्गमूल, घनमूल, आदि) पूरी तरीके से नहीं निकाला जा सकता है उस संख्या को करणी (Surds) कहते है। यही करणी की परिभाषा (Surds Definition) भी है।

उदाहरण (Example): √2, √3, √5, ∛7, ∛5 आदि करणी के उदाहरण है।

Note: √4, √16, √25, ∛27, ∛8 करणी नहीं है। क्योकि इनको आगे हल करके उत्तर मिल सकता है। नीचे हल देखे-

√4 = 2
√16 = 4
√25 = 5
∛27 = 3
∛8 = 2

इसका अर्थ है कि √4 को 2, √16 को 4, √25 को 5, ∛27 को 3, ∛8 को 2 में हल कर सकते है।

power, indices and surds formula — **Power, Indices and Surds Formula**

Important Topics

Surds Formula and Rules

1.) Surds को जोड़ना व घटाना (Addition and Subtraction of Surds)

Surds को जोड़ने की के नियम में केवल समान सर्ट्स (Same Radicand) ही जोड़े और घटाए जा सकते हैं। उदाहरण (Example):

Surds को जोड़ना उदाहरण: 7√5 + 2√5 = 9√5
Surds को घटाना उदाहरण: 9√7 – 3√7 = 6√7

Note: Surds को जोड़ने व घटाने के कार्य में केवल समान प्रकार (जिनमें मूल Root के अंदर का भाग समान होता है ) को ही जोड़ा व घटाया जा सकता है।

2.) Power, Surds and Indices Multiplication (Surds की गुणा)

Surds की गुणा करने के नियम में Surds का समान होना आवश्यक नही होता है। उदाहरण (Example):

Surds की गुणा करना उदाहरण: √5 × √2 = √10
No. 2 Example: √7 × √5 = √35
No. 3 Example: 2√3 × 3√5 = 6√15
(मूल के बाहर की संख्याओं की आपस में गुणा तथा मूल के अंदर की संख्याओं की आपस में गुणा की जाती है।)

3.) Surds का भाग (Division of Surds)

Surds के भाग करने के नियम में भी इनका समान होना आवश्यक नहीं होता है। उदाहरण (Example):

Surds का भाग करना उदाहरण: √12 ÷ √2 = √6
No. 2 Example: √15 × √5 = √3

Power, Indices and Surds Questions and Answers

Question 1: नीचे दी गयी गणितीय संक्रिया में x का मान ज्ञात करें।
Find the Value of x in the below expression. $$2^{2x – 1} = \frac{1}{8^{x – 3}}$$

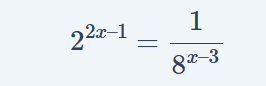
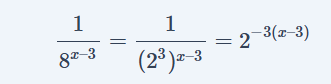
Answer 1: हम जानते है कि 2³=8 होता है इसलिए $$\frac{1}{8^{x – 3}} = \frac{1}{(2^3)^{x – 3}} = 2^{-3(x – 3)}$$ प्राप्त होता है। इसे प्रश्न में रखने पर-

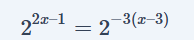
$$2^{2x – 1} = 2^{-3(x – 3)}$$ Rule 1 के अनुसार, हम जानते है कि निचले पद समान होने पर घाते भी समान होती है। अतः

2x-1 = -3(x-3)
2x-1 = -3x+9
2x+3x = 9+1
5x = 10
x = 10 ÷ 5
x = 2

Question 2: अगर 3^x+y=81, 81^x-y=3 हो तो x और y का मान ज्ञात करें।
(If 3^x+y=81, 81^x-y=3 then find the value of x and y.)

Answer 2: Given,
3^x+y = 81
3^x+y = 3⁴
base समान है इसलिए घात समान होगी। तो x+y = 4 ……… Equation (1)

इसी प्रकार, 81^x-y = 3
3^4(x-y) = 3¹
Base समान है तो घात बराबर होगी। अतः
4(x-y) = 1
x-y = 1/4 ……. Equation (2)

1 समीकरण (x+y= 4) और 2 समीकरण (x-y = 1/4) को जोड़ने पर- $$2x = 4 + \frac{1}{4}$$
$$ 2x = \frac {16+1} {4} $$
$$ 2x = \frac {17} {4} $$
$$ x = \frac {17} {8} $$
x का मान 1 समीकरण x+y = 4 में रखने पर-
$$ \frac {17} {8} + y = 4 $$
$$ y = 4 – \frac {17} {8} $$

$$ y = \frac {32-17} {8} $$
$$ y = \frac {15} {8} $$

Answer: $$ x = \frac {17} {8} $$ and $$ y = \frac {15} {8} $$

Watch Power, Indices and Surds Video:

Click Here

Join Us Now

0 +

Helping more than 10,000 students

Latest Posts: