प्रकाश के एक माध्यम से दूसरे माध्यम में जाने पर अपने मार्ग से विचलित होने की प्रक्रिया को प्रकाश का अपवर्तन (Refraction of Light) कहते है। प्रकाश के अपवर्तन की खोज का श्रेय डच खगोलशास्त्री और गणितज्ञ विलेब्रोर्ड स्नेलियस (Willebrord Snellius) को जाता है। इस आर्टिकल में हम प्रकाश का अपवर्तन, स्नैल का नियम, अपवर्तन के नियम, क्रान्तिक कोण (Critical Angle), पूर्ण आन्तरिक परावर्तन (Total Internal Reflection), क्रान्तिक कोण तथा अपवर्तनांक में सम्बन्ध को उदाहरण सहित समझेंगे।
प्रकाश का अपवर्तन (Refraction of light)
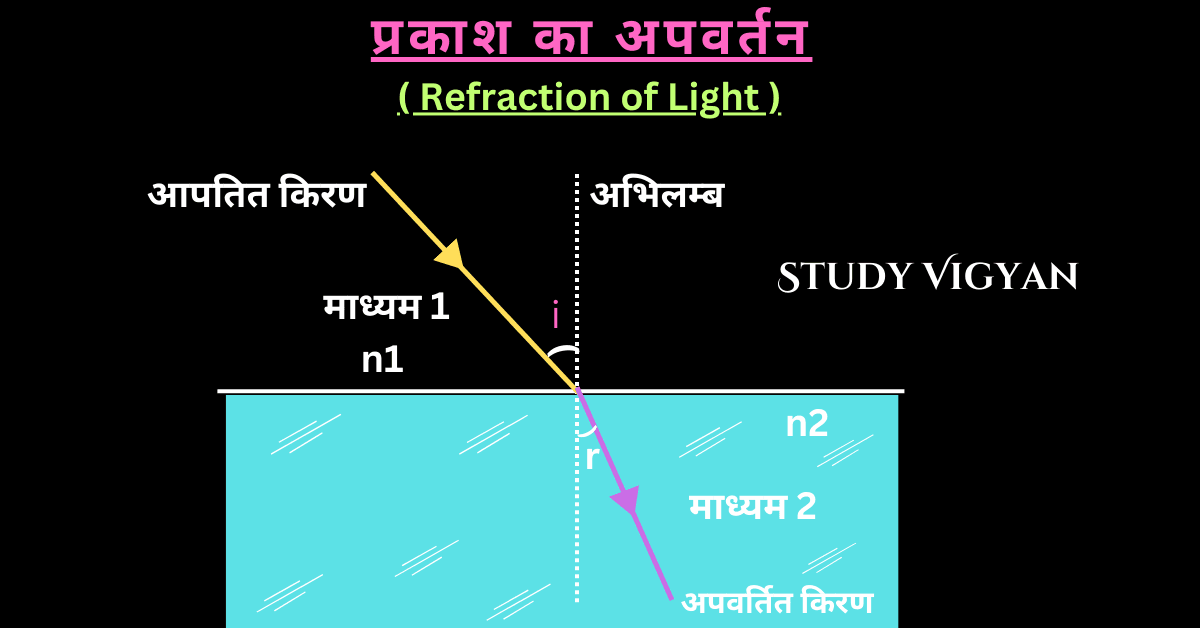
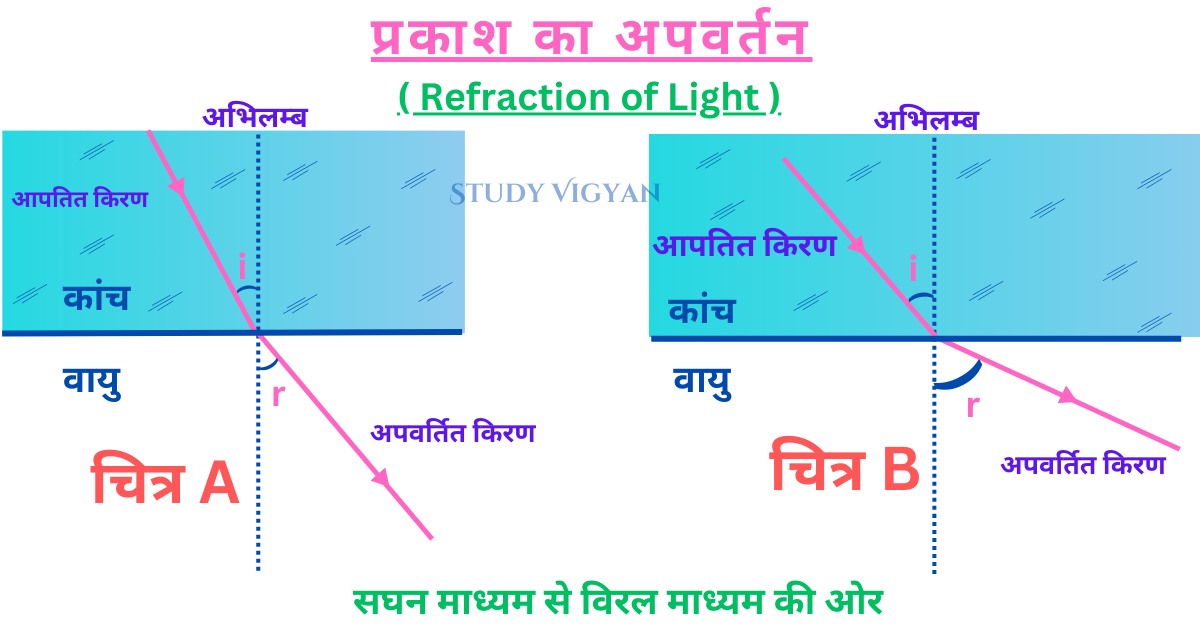
जब प्रकाश की किरण एक माध्यम से किसी दूसरे माध्यम में प्रवेश करती है तो वह अपने मार्ग से कुछ विचलित हो जाती है, प्रकाश की इस घटना को प्रकाश का अपवर्तन (Refraction of light) कहते है।
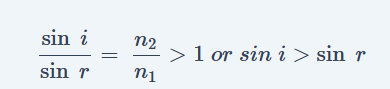
- यदि प्रकाश किरण विरल माध्यम से सघन माध्यम की और जा रही है तो किरण अभिलम्ब के पास आती है। अतः $$ n_2>n_1$$ तो $$ \frac{\sin\;i}{\sin\;r}=\;\frac{n_2}{n_1}>1\;or\;sin\;i>\sin\;r\; $$ $$ i>r$$
- यदि प्रकाश किरण सघन माध्यम से विरल माध्यम की और जा रही है तो किरण अभिलम्ब से दूर हटती है। अतः
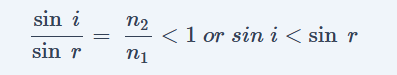
$$ \frac{\sin\;i}{\sin\;r}=\;\frac{n_2}{n_1}<1\;or\;sin\;i<\sin\;r\; $$ $$ r>i $$
अपवर्तन के नियम (Law of Refraction)
अपवर्तन के मुख्य रूप से दो नियम होते है जो निम्न प्रकार है-
1.) अपवर्तन का पहला नियम (Refraction First Law)
आपतित किरण, आपतन बिंदु पर अभिलम्ब तथा अपवर्तित किरण तीनो एक ही तल में होते है।
2.) स्नैल का नियम (Snell’s law) या अपवर्तन का दूसरा नियम
प्रकाश के अपवर्तन में आपतन कोण (i) की ज्या sine तथा एक निश्चित तरंगदैर्ध्य के लिए अपवर्तन कोण (r) की ज्या sine की निष्पत्ति (का अनुपात) नियत रहता है, इसे ही स्नैल का नियम (Snell’s Law) कहते है। इसे अपवर्तन का दूसरा नियम भी कहा जाता है।
$$ \frac{\sin\;i}{\sin\;r}=1\eta2=\frac{n_1}{n_2}=\mathrm{ constant } $$
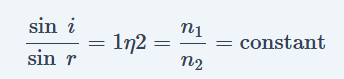
इसे ही स्नैल के नियम का सूत्र कहलाता है।
जिसमे $$ {}_1n_2\;=\;\frac{n_2}{n_1} $$, पहले माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक (Refractive Index) है। अपवर्तनांक एक सापेक्ष गुण है। यह सदैव दो माध्यमों के मध्य निकाला जाता है।
निरपेक्ष अपवर्तनांक (Absolute refractive Index): निर्वात के सापेक्ष निकाले गए किसी माध्यम के अपवर्तनांक को निरपेक्ष अपवर्तनांक कहते है।
n1= प्रथम माध्यम का अपवर्तनांक है।
n2= दूसरे माध्यम का अपवर्तनांक है।
नोट (Note)-
- किसी माध्यम का अपवर्तनांक उस माध्यम की प्रकृति, आपतित प्रकाश की तरंगदैर्ध्य तथा ताप पर निर्भर करता है।
- एक माध्यम से दूसरे माध्यम में जाने पर आपतित किरण की आवृत्ति वही रहती है लेकिन उसका वेग बदल जाता है।
- एक माध्यम से दूसरे माध्यम में जाने पर आपतित किरण की आवृत्ति वही रहती है लेकिन उसका तरंगदैर्ध्य (λ) बदल जाता है।
- यदि कोई किरण अभिलम्ब से होकर जाती है तो वह किरण सीधे निकल जाती है। अतः i=0 है तो वह किरण सीधे निकल जाएगी तो r=0 होगा।
अपवर्तन के उदाहरण (Refraction Examples)
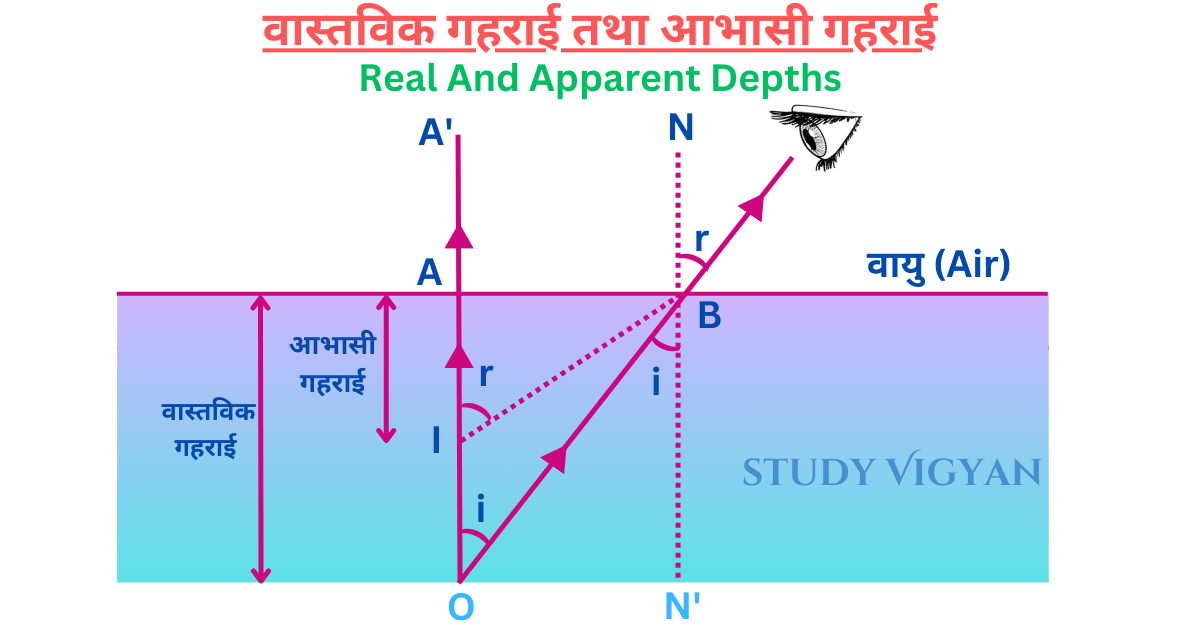
- जल में पड़े सिक्के या किसी वस्तु का कुछ उठा हुआ प्रतीत होना- यदि कोई सिक्का किसी पानी से भरी बाल्टी की तली में रखा है तो यह सिक्का बाल्टी में कुछ ऊपर की ओर उठा हुआ दिखाई पड़ता है। यह घटना अपवर्तन के कारण ही होती है। जल में पड़ा सिक्का अपनी वास्तविक गहराई से कुछ कम गहरा दिखाई पड़ता है।
अतः किसी वस्तु के जल या अन्य किसी द्रव में गिरे रहने पर उसकी वास्तविक गहराई को निम्न सूत्र द्वारा ज्ञात कर सकते है-
$${}_an_w=\;\frac{Real\;Depth}{Virtual\;Depth}$$
Real Depth= वास्तविक गहराई
Virtual Depth= आभासी गहराई
- क्रान्तिक कोण का बनना तथा पूर्ण आन्तरिक परावर्तन की घटना अपवर्तन के कारण ही संभव है।
- जल में परखनली का चमकीला दिखाई देना, कांच में पड़ी दरारों का चमकना, हीरे का चमकना प्रकाश के अपवर्तन तथा पूर्ण आन्तरिक परावर्तन के ही उदाहरण है।
- रेगिस्तान में मरीचिका का दिखना, ठन्डे प्रदेशो में मरीचिका का दिखना, प्रकाशिक तन्तु प्रकाश के अपवर्तन तथा पूर्ण आन्तरिक परावर्तन के उदाहरण है।
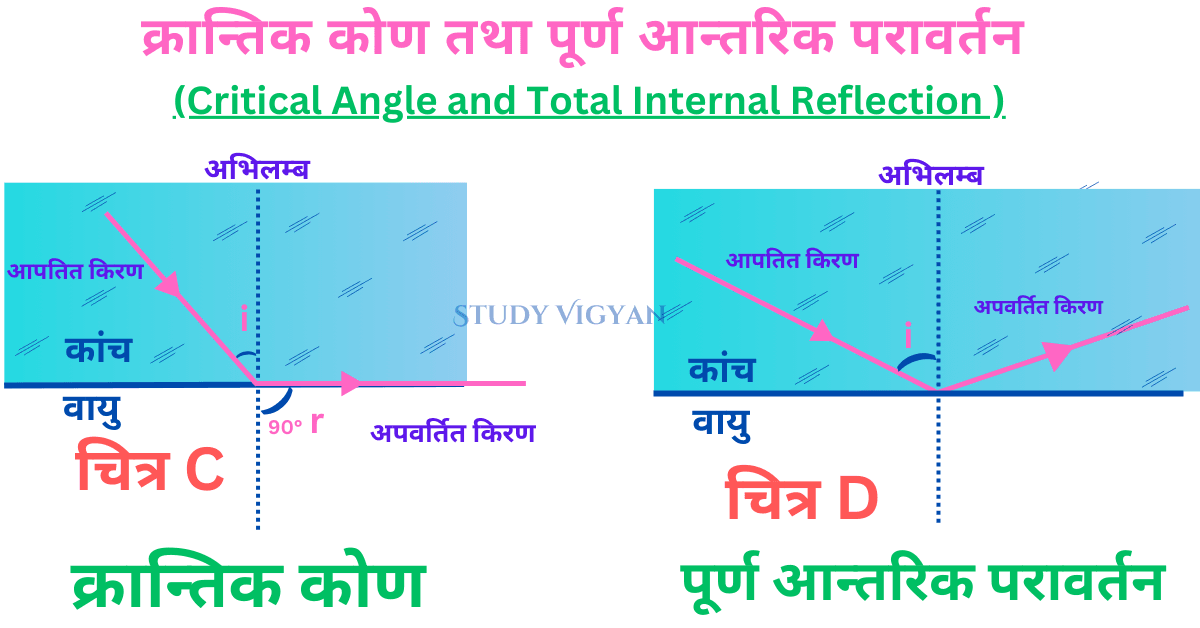
क्रान्तिक कोण की परिभाषा व सूत्र (Critical Angle Definition, Formulas)
परिभाषा: सघन माध्यम में बना वह आपतन कोण जिसके लिए विरल माध्यम में बने अपवर्तन कोण का मान 90 होता है क्रान्तिक कोण (Critical Angle) कहलाता है। यही क्रान्तिक कोण की परिभाषा कहलाती है।
शर्त (condition)- 1.) क्रान्तिक कोण का बनना तभी संभव है जब प्रकाश किरण सघन माध्यम से विरल माध्यम की ओर जा रही हो।
2.) अपवर्तन कोण का मान 90 होना चाहिए।
क्रान्तिक कोण को समझना (Critical Angle Properties)
- चित्र के अनुसार कोई किरण OA सघन माध्यम से विरल माध्यम की ओर जा रही है।
- हम जानते है जब किरण सघन माध्यम से विरल माध्यम में जाती है तो अभिलम्ब से दूर हटती है। चित्र (Fig) A
- अब यदि हम आपतन कोण (i) को थोड़ा ओर बढ़ाते है तो अपवर्तन कोण (r) ओर अधिक बढ़ जाता है अतः किरण अभिलम्ब से ओर अधिक दूर जाती है। (चित्र B)
- अब यदि हम आपतन कोण (i) को थोड़ा ओर बढ़ाते है ओर देखते है कि अपवर्तित किरण अभिलम्ब से दूर हटती है जिससे अपवर्तन कोण (r) का मान 90 हो गया है। (चित्र C)
- अतः वह स्तिथि जब अपवर्तन कोण (r) का मान 90 डिग्री हो जाता है तो आपतन कोण (i) को क्रान्तिक कोण कहते है।
पूर्ण आन्तरिक परावर्तन (Total Internal Reflection)
परिभाषा: जब प्रकाश किरण सघन माध्यम से विरल माध्यम में जा रही हो और विरल माध्यम में बने अपवर्तन कोण का मान 90° से अधिक होता है तो प्रकाश किरण पुनः सघन माध्यम में ही लौट आती है, प्रकाश की इस घटना को प्रकाश का पूर्ण आन्तरिक परावर्तन (Total Internal Reflection) कहते है।
ऊपर चित्र D में आपतन कोण को इतना बढ़ाया गया है कि अपवर्तित किरण विरल माध्यम में जाए बिना पुनः सघन माध्यम में लौट आती है, यही घटना पूर्ण आन्तरिक परावर्तन कहलाती है।
शर्त (Condition)- 1.) प्रकाश सघन माध्यम से विरल माध्यम में जा रहा हो।
2.) आपतन कोण क्रान्तिक कोण से बड़ा हो।
पूर्ण आन्तरिक परावर्तन (Total Internal Reflection) को समझना
जिस प्रकार हमने क्रान्तिक कोण को समझा था उसी प्रकार यदि हम आपतन कोण को क्रान्तिक कोण के आ जाने के बाद थोड़ा ओर बढ़ाते है तो हम देखेंगे कि कोई प्रकाश किरण अपवर्तन के पश्चात विरल माध्यम में नहीं जाता है। बल्कि संपूर्ण प्रकाश पुनः सघन माध्यम में लौट जाता है। इसमें प्रकाश का अपवर्तन न होकर परावर्तन ही होता है। इसी कारण प्रकाश की इस घटना को पूर्ण आंतरिक परावर्तन (Total Internal Reflection) कहते है।
पूर्ण आन्तरिक परावर्तन का उदाहरण व उपयोग (Total Internal Reflection Examples and Uses)
जल में रखी परखनली का चमकना, कांच में पड़ी दरारों का चमकना, हीरे का चमकना, रेगिस्तान में मरीचिका का दिखना, ठंडे प्रदेशो में मरीचिका का दिखना, प्रकाशिक तन्तु इत्यादि पूर्ण आंतरिक परावर्तन के उदाहरण व उपयोग है जिन्हे हमने विस्तार से Image व Video के माध्यम से बेहतरीन ढंग से समझाया गया है। नीचे क्लिक करके बेहतरीन ढंग से समझे-
क्रान्तिक कोण तथा अपवर्तनांक में सम्बन्ध (Relation between Critical Angle and Refractive Index)
यदि विरल माध्यम को 1 तथा सघन माध्यम को 2 द्वारा प्रदर्शित किया जाये तो स्नैल के नियमानुसार, सघन माध्यम के सापेक्ष विरल माध्यम का अपवर्तनांक-
$${}_2n_1=\;\frac{\sin\;i}{\sin\;r}$$
यदि आपतन कोण i = क्रान्तिक कोण c तथा अपवर्तन कोण r = 90 हो तो
$${}_2n_1=\;\frac{\sin\;c}{\sin\;90}$$
परन्तु $${}_2n_1=\;\frac1{{}_1n_2}$$ जहा 1n2 विरल माध्यम के सापेक्ष सघन माध्यम का अपवर्तनांक है
$$ \frac1{{}_1n_2}=\;\sin\;c $$
$$ {}_1n_2=\frac1{\sin\;c} $$
यदि प्रकाश कांच से वायु में जा रहा हो तो वायु के सापेक्ष कांच का अपवर्तनांक-
$${}_an_g=\frac1{\sin\;c}$$
अतः यदि कांच वायु के लिए क्रान्तिक कोण ज्ञात हो तो कांच का अपवर्तनांक ज्ञात किया जा सकता है
कांच वायु के लिए क्रान्तिक कोण (C) 41°49′ तथा जल वायु के लिए क्रान्तिक कोण (C) 48°39′ होता है।
प्रकाश का अपवर्तन का विस्तार से वर्णन-
प्रकाश के अपवर्तन, स्नैल के नियम, क्रान्तिक कोण, पूर्ण आन्तरिक परावर्तन, अपवर्तनांक तथा क्रान्तिक कोण में सम्बन्ध ये सभी टॉपिक परीक्षा की दृष्टि से अत्यंत महत्वपूर्ण है। इनसे परीक्षा में कई लिखित तथा बहुविकल्पीय पूछे जाते है।
इसके अलावा अवतल तथा उत्तल दर्पण के उपयोग व उदाहरण जानें।
- International Men’s Day 2024: इंटरनेशनल मेन्स डे कब मनाया जाता है?, क्या होता है? क्यों मनाया जाता है?, इंटरनेशनल मेन्स डे 2024 थीम, कैसे मनाया जाता है?, महत्व जानें
- इंजीनियरिंग ड्राइंग में रेखाएं कितने प्रकार की होती है?, इंजीनियरिंग ड्राइंग में रेखा किसे कहते है?, विभिन्न रेखाओं के उपयोग, विशेषता, मोटाई, उदाहरण चित्र सहित जानें
- Ibps rrb po mains result 2024 कैसे चेक करें? इंटरव्यू कितने अंक का होता है? महत्वपूर्ण जानकारी
- इंजीनियरिंग ड्राइंग में टाइटल ब्लॉक को कैसे बनाते हैं?, टाइटल ब्लॉक का डिज़ाइन, आकार, प्रकार, परिभाषा, 8 जरुरी सावधानियों को जानें
- न्यूटन का पहला नियम (Newton’s First Law): परिभाषा, कारण, अनुप्रयोग, उदाहरण | जड़त्व का नियम (Law of Inertia), प्रकार
- विकृति ऊर्जा (Strain Energy) की परिभाषा, सूत्र, निगमन, मात्रक और ऊर्जा गुणांक को चित्र सहित जानें | प्रमाण विकृति ऊर्जा, प्रमाण प्रतिबल, विकृति क्या होते है?
- गुणोत्तर श्रेणी (Geometric Progression): परिभाषा, गुणोत्तर श्रेणी के सूत्र, योग, सवाल व गुणोत्तर माध्य को उदाहरण सहित
- केशिकत्व (Capillarity): परिभाषा, सिद्धांत, उदाहरण, सूत्र और प्रैक्टिकल
- जल में पड़े सिक्के या वस्तु का कुछ उठा हुआ प्रतीत होना
- आपदा: परिभाषा, प्रकार, उदाहरण, प्रभाव | प्राकृतिक और मानवकृत आपदा के कारण
- प्रकाश का अपवर्तन (Refraction of Light): अर्थ, परिभाषा, अपवर्तन के नियम, स्नैल का नियम, सूत्र तथा क्रान्तिक कोण तथा पूर्ण आन्तरिक परावर्तन को उदाहरण सहित समझे
