वृत्तीय गति किसे कहते है? वृत्तीय गति के उदाहरण, परिभाषा, सूत्र, कोणीय विस्थापन, कोणीय वेग तथा रेखीय वेग में सम्बन्ध

वृत्तीय गति में कण वृत्तीय पथ पर गति करता है। वृतीय गति के उदाहरण दैनिक जीवन में भी देखने को भी मिलते है। यदि हम डोरी के एक सिरे पर वस्तु को बाँधकर क्षैतिज वृत्त में घुमाए तो उसकी गति भी वृतीय गति कहलाती है।

एक लेख में हम वृत्तीय गति की परिभाषा, सूत्र, चित्र, कोणीय विस्थापन, कोणीय वेग तथा रेखीय वेग में सम्बन्ध को बेहतरीन ढंग से चित्र सहित समझेंगे। इसके साथ वृत्तीय गति के उदाहरण और दैनिक जीवन में वृत्तीय गति को भी बताया गया है।

वृत्तीय गति (Circular Motion)

जब कोई कण एक निश्चित बिन्दु (point) को केन्द्र मानकर उसके चारों एक वृत्तीय पथ पर गति करता है तो उस कण की गति वृत्तीय गति (Circular Motion) कहलाती है।

नोट: वृत्तीय गति समतल गति के अंतर्गत आती है। वृत्तीय गति में परिणाम अचर (constant) होता है, लेकिन दिशा लगातार बदलती रहती है।

एक समान वृत्तीय गति: यदि कण की वृत्तीय पथ पर चाल अचर (constant) रहती है तो कण की गति एक समान वृत्तीय गति कहलाती है।

वृत्तीय गति का चित्र सहित समझना

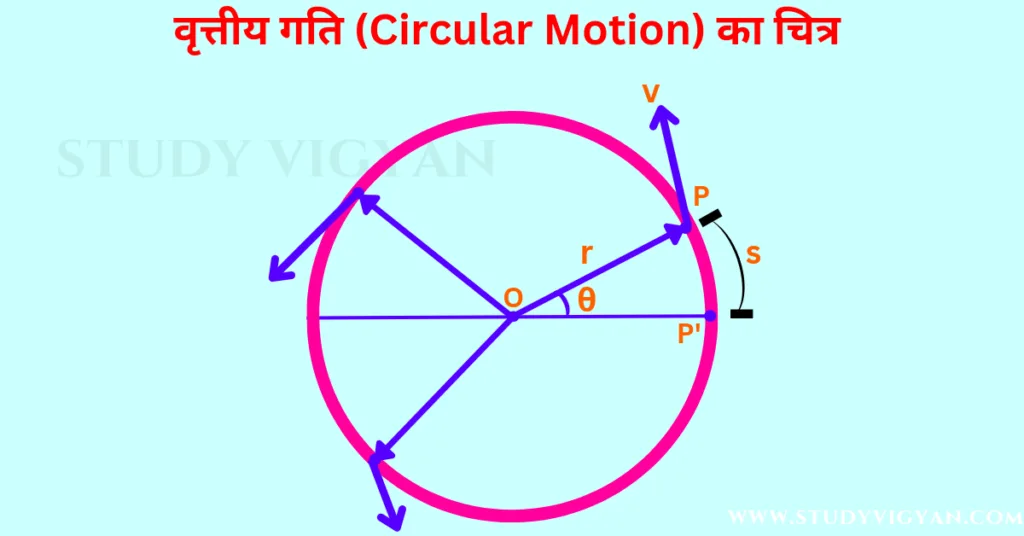
चित्र में कण P वृत्तीय गति कर रहा है। यह कण बिन्दु O के चारों ओर अचर चाल v से चल रहा है।

• θ= कण की वृत पर स्थिति कोण θ द्वारा बता सकते है। यह कोण त्रिज्य रेखा OP तथा स्थिर रेखा OP’ के बीच बनता है।
• वेक्टर OP’= सदिश OP’ कण P की तात्कालिक स्थिति प्रदर्शित करता है।
• वेक्टर r= कण P का त्रिज्य सदिश है। इसका परिमाण वृत्त की त्रिज्या के बराबर तथा दिशा केन्द्र के ओर रहती है।
• वेक्टर v= वृत्तीय गति में वृत्त के किसी बिंदु से खींचे गए स्पर्शरेखीय सदिश को उस बिंदु पर कण का रेखीय वेग सदिश कहते है। इसका परिणाम तो स्थिर रहता है लेकिन दिशा लगातार बदलती रहती है।

वृत्तीय गति के उदाहरण | वृत्तीय गति के 5 उदाहरण

1. वस्तु को डोरी में बाँधकर क्षैतिज वृत्त में घुमाना- जब हम किसी हल्की वस्तु को डोरी में बाँधकर क्षैतिज वृत्त में घुमाते है तो डोरी के तनाव द्वारा वस्तु पर अभिकेन्द्र बल कार्य करने लगता है। इस प्रकार वृत्तीय गति उत्पन्न होती है। अभिकेंद्र बल की दिशा सदैव केन्द्र की ओर होती है।

2. कार का सड़क पर मुड़ना- जब कोई कार सड़क के मोड़ पर पहुँचती है तो उसे मुड़ने के लिए अभिकेन्द्र बल की आवश्यकता होती है। मुड़ने के लिए कार को यह अभिकेन्द्र बल टायर तथा सड़क के बीच घर्षण बल से प्राप्त होता है। यदि गाड़ी के टायर घिसे हुए है या सड़क फिसलन वाली है तो कार को पर्याप्त घर्षण बल नहीं मिल पाता है। इससे कार को मोड़ पर अभिकेन्द्र बल नहीं मिलता और कार फिसल जाती है।

3. साइकिल तथा गाड़ियों में मड गार्ड- जब कीचड़ वाली सड़क पर तेज गति से गाड़ी गुजरती है तो कीचड़ के कण गाड़ी के टायर से चिपक जाते है और कीचड़ के कण ऊपर की ओर टायर के स्पर्श-रेखा की दिशा में फेंक दिए जाते है। अतः गाड़ी के पीछे का हिस्सा गन्दा न हो इसीलिए गाड़ियों में मड गार्ड लगाए जाते है।

4. पृथ्वी का सूर्य के चारों ओर घूमना- पृथ्वी सूर्य के चारों ओर घूमती है इसमें भी अभिकेन्द्र बल कार्य करता है। इस अभिकेंद्र बल की दिशा वृत्त के केन्द्र की ओर होती है। यह भी वृत्तीय गति का उदाहरण है।

5. इलेक्ट्रान का नाभिक में घूमना- परमाणु में नाभिक के चारों ओर इलेक्ट्रान वृत्तीय कक्षाओं में घूमते है। इन इलेक्ट्रानो पर केन्द्र की ओर एक अभिकेंद्रीय बल कार्य कार्य करता है। नाभिक पर धन आवेश होता है तथा इलेक्ट्रान पर ऋण आवेश होता है। इसके बीच स्थिर वैधुत आकर्षण बल होता है। यह बल ही घूमने के लिए अभिकेन्द्र बल का कार्य करता है। अतः यह भी वृत्तीय गति का उदाहरण है।

कोणीय विस्थापन (Angular Displacement) | कोणीय विस्थापन की परिभाषा

जब कोई कण किसी वृत्त की परिधि पर चल रहा है तब कण का त्रिज्य वेक्टर (r) कण की प्रारम्भिक स्थिति से जितने कोण पर घूम जाता है, उस कोण को कण का कोणीय विस्थापन (Angular Displacement) कहते है। यही कोणीय विस्थापन की परिभाषा भी है।

कोणीय विस्थापन को ∆θ से प्रदर्शित करते है। यह एक सदिश राशि है। कोणीय विस्थापन का मात्रक रेडियन होता है।

कोणीय विस्थापन का सूत्र | Angular Displacement Formula

कोणीय विस्थापन का सूत्र= $$\mathrm{Angular}\;\mathrm{Displacement}\;\triangle\mathrm\theta\;=\frac{\triangle\mathrm s\;}{\mathrm r}$$

• ∆θ= कोणीय विस्थापन
• ∆s= वृत्तीय पथ पर चली गयी दूरी
• r= वृत्तीय पथ की त्रिज्या

यह सूत्र कोण= चाप/त्रिज्या के सिद्धान्त से आता है। यह सूत्र ही कोणीय विस्थापन और रेखीय विस्थापन में संबंध है।

कोणीय विस्थापन का उदाहरण चित्र सहित

कण वृत्त की परिधि पर anticlockwise (वामावर्त) दिशा में चल रहा है। कण वृत्त के बिंदु P’ से चलना शुरू करता है। समय t1 पर कण की स्थिति θ1 तथा समय t2 पर कण की स्थिति θ2 है।

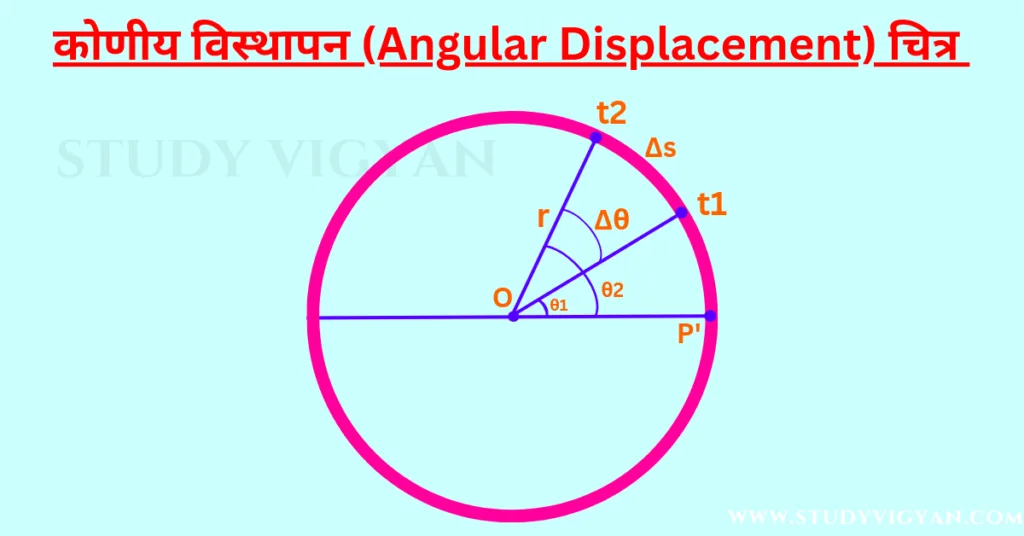
इस समयांतराल ∆t (t2-t1) में कण ∆s दूरी चलता है। इस ∆s को ही रेखीय विस्थापन कहते है क्योंकि यह समय t1 से t2 के बीच anticlockwise दिशा में वृत्त के चाप पर चली गई दूरी है। इस दौरान कण कोण θ2-θ1=∆θ घूम जाता है। कण का यह घुमाव कोण ∆θ ही कोणीय विस्थापन कहलाता है।

Join us Now

• WhatsApp
• Telegram
• Instagram

कोणीय वेग (Angular velocity)

जब कोई कण किसी वृत्त की परिधि पर चलता है तो कण का कोणीय विस्थापन समय के साथ बदलता रहता है।

कोणीय वेग की परिभाषा- कोणीय विस्थापन की समय के साथ परिवर्तन दर को कोणीय वेग कहते है। इसे ω (ओमेगा) से प्रदर्शित करते है। कोणीय वेग का मात्रक रेडियन/सेकंड होता है। इसकी विमा ${\mathrm{M0L0T<mo>-1</mo>}}^{}$ होती है।

कोणीय वेग का सूत्र (Angular velocity formula)

यदि समयान्तराल ∆t में कण का कोणीय विस्थापन ∆θ हो तो कण का कोणीय वेग (Angular velocity) का सूत्र=$$\mathrm{Angular}\;\mathrm{Velocity}\;(\mathrm\omega)\;=\frac{\triangle\mathrm\theta\;}{\triangle\mathrm t\;}$$

इस सूत्र में यदि कण एक पूरा चक्कर घूम रहा हो तो ∆ω= 2π होगा जो 360° के बराबर होता है।
T= कण द्वारा लिया गया 1 चक्कर में लिया गया समय है जो परिक्रमण काल कहलाता है। इसे T से प्रदर्शित करते है।

अतः कण का औसत कोणीय वेग=

$$\omega=\;\frac{2\;\mathrm\pi}{\mathrm T}$$

n=1/T होता है अतः-

यदि कण 1 सेकण्ड में n चक्कर लगाए तो कण का औसत कोणीय वेग= $$\omega=\;2\;\mathrm\pi\;\mathrm n\;$$

• n= कण की आवृति
• ω= कोणीय वेग

यह भी जाने-

• पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन

• पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन

रेखीय वेग (Linear Velocity) | रेखीय वेग की परिभाषा

सरल रेखीय गति में किसी कण के रेखीय विस्थापन को समय के साथ परिवर्तन-दर को उस कण का रेखीय वेग कहते है।
जब कोई कण सरल रेखीय गति करता है तो उसका रेखीय विस्थापन समय के साथ-साथ बदलता रहता है।

यही रेखीय वेग की परिभाषा है। रेखीय वेग का मात्रक मीटर/सेकण्ड होता है। रेखीय वेग सदिश राशि है। इसकी विमा L T-1 होती है।

रेखीय वेग का सूत्र

यदि एक सूक्ष्म समयांतराल ∆t में कण का रेखीय विस्थापन ∆s हो तो कण का औसत रेखीय वेग का सूत्र= $$v=\frac{\triangle s}{\triangle t}$$ यदि समयान्तराल अत्यंत सूक्ष्म हो तो कण का औसत रेखीय वेग तात्कालिक रेखीय वेग के बराबर होगा अतः रेखीय वेग का सूत्र = $$v=\frac{ds}{dt}$$

कोणीय वेग तथा रेखीय वेग में संबंध | Relation between Angular velocity and Linear velocity

कण वृत्त की परिधि पर ∆t समय में ∆s दूरी तय करता है तो हम जानते है कि कण के कोणीय विस्थापन का सूत्र= $$\triangle\theta=\frac{\triangle s}{r\;}$$ दोनों ओर ∆t से भाग करने पर- $$\frac{\triangle\theta}{\triangle t\;}=\frac{1\;}{r\;}\frac{\triangle s}{\triangle t\;\;}$$ हम जानते है कि-

$$\omega=\frac{\triangle\theta}{\triangle t\;}\;and\;v=\frac{\triangle s\;}{\triangle t\;}$$ यह मान ऊपर समीकरण में रखने पर- $$\omega=\frac vr$$ $$\left[v=r\;\omega\right]$$

यह सूत्र ही कोणीय वेग और रेखीय वेग का सम्बन्ध है।

वृत्तीय गति का आवर्तकाल

कण द्वारा 1 चक्कर पूरा करने में लगे समय को आवर्तकाल कहते है। इसे T से प्रदर्शित करते है। इसका मात्रक सेकंड होता है।

हम जानते है समय= दूरी/चाल होता है। अतः आवर्तकाल (T)=

आवर्तकाल (T)= एक चक्कर में चली गयी दूरी/चाल

आवर्तकाल का सूत्र (T)= 2πr / v

FAQ (Frequently Asked Questions)-

वृत्तीय गति (Circular Motion) का वीडियो सहित समझना