पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन | Gravitational Acceleration above the Earth Surface

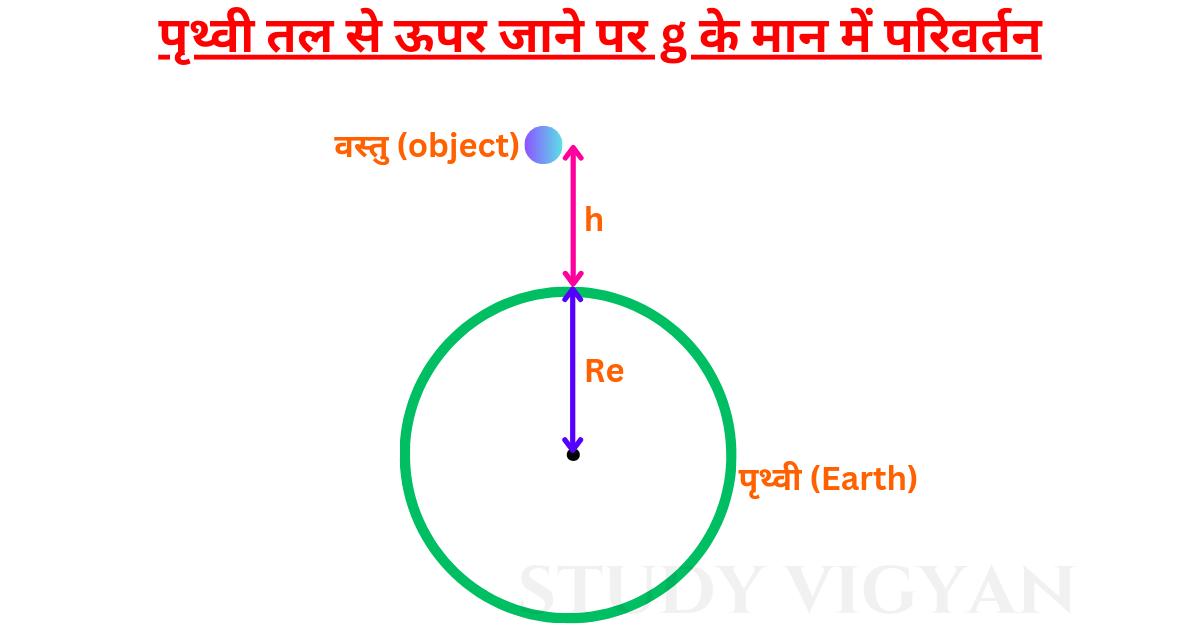
पृथ्वी तल पर g (गुरुत्वीय त्वरण) का मान 9.81 मीटर/सेकंड² होता है। पृथ्वी तल से ऊपर तथा नीचे जाने में g का मान घटता है। पृथ्वी तल से ऊपर जाने में g का मान घटता जाता है जैसे-जैसे ऊंचाई बढ़ती जाती है उसी तरह से g गुरुत्वीय त्वरण का मान कम होता जाता है।

पृथ्वी तल से ऊपर जाने में g का मान क्यों घटता है? इसका कारण, सूत्र, संबंध हम सरल भाषा में समझेंगे। इसके साथ पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन का सूत्र भी स्थापित करेंगे।

पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन का सूत्र

$$g’=\frac1{\left(1+{\displaystyle\frac h{R_e}}\right)^2}$$

यहाँ,

• g’= ऊपर जाने पर परिवर्तित गुरुत्वीय त्वरण
• g = पृथ्वी तल पर गुरुत्वीय त्वरण
• h = पृथ्वी से तल से वस्तु की ऊंचाई
• Re= पृथ्वी की त्रिज्या

समझने के लिए: हम एक वस्तु को पृथ्वी तल से h ऊंचाई पर ले गए है। इस स्थान पर हम वस्तु का परिवर्तित गुरुत्वीय त्वरण (g’) ऊपर दिए सूत्र की सहायता से ज्ञात कर सकते है। पृथ्वी तल पर g (गुरुत्वीय त्वरण) का मान 9.81 मीटर/सेकंड² होता है।

पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन सूत्र का निगमन (सम्बन्ध)

पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन सूत्र का निगमन (सम्बन्ध) करने से पहले हमें कुछ बातों का पता होना जरुरी है। जैसे-

• O = पृथ्वी का केंद्र
• Me = पृथ्वी का द्रव्यमान
• m = वस्तु का द्रव्यमान
• g’= ऊपर जाने पर परिवर्तित गुरुत्वीय त्वरण
• g = पृथ्वी तल पर गुरुत्वीय त्वरण
• h = पृथ्वी से तल से वस्तु की ऊंचाई
• Re= पृथ्वी की त्रिज्या

स्थिति (1) पृथ्वी के तल पर m द्रव्यमान की एक वस्तु स्थित है।

न्यूटन के गुरुत्वाकर्षण नियम के अनुसार,
(यदि आप गुरुत्वाकर्षण बल तथा उसके सूत्र के बारे में जानना चाहते है तो कमेंट बॉक्स में लिखे)

समीकरण (1) वस्तु पर कार्य करने वाला गुरुत्व बल (F)=
$$F=\frac{G\;M_e\;m}{R_e^2}$$

समीकरण (2) वस्तु का भार (W)=
$$W=m\;g$$

समीकरण 1 व समीकरण 2 से-
$$m\;g=\frac{G\;M_{e\;}m}{{R^2}_e}….\;Equation\;(3)$$

स्थिति (2) जब वस्तु को पृथ्वी तल से h ऊँचाई पर ले जाते है।

तो समीकरण 3 की तरह ऊंचाई (h) पर वस्तु का समीकरण-

$$m\;g’=\frac{G\;M_{e\;}m}{\left(R_e+h\right)^2}…\;Equation\;(4)$$

समीकरण 4 को समीकरण 3 से भाग देने पर-
$$\frac{m\;g’}{m\;g}=\frac{\frac{G\;M_{e\;}m}{\left(R_e+h\right)^2}}{\frac{G\;M_{e\;}m}{\left(R_e+h\right)^2}}$$

भाग के ऊपर वाला m, G, Me नीचे वाले m, G, Me से विभाजित (कट) जाएगा। अतः
$$\frac{g’}g=\frac{R_e^2}{\left(R_e+h\right)^2}$$

ऊपर दिए गए समीकरण को Re के वर्ग से भाग देने पर-
$$\frac{g’}g=\frac1{\left(1+{\displaystyle\frac h{R_e^2}}\right)^2}$$
$$g’=\frac g{\left(1+{\displaystyle\frac h{R_e^2}}\right)^2}$$

यही समीकरण पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन का सूत्र (सम्बन्ध) है।

इस समीकरण से हम देख सकते है कि g’ के सामने g है। g के भागफल में ऊँचाई (h) है। अतः समीकरण में ऊँचाई h के बढ़ने पर g के मान में कमी आती है। जिससे g’ का मान भी कम आएगा क्यूंकि यह g के बराबर में है।

g'<g

इससे यह सिद्ध होता है कि पृथ्वी तल से ऊँचाई पर जाने में g (गुरुत्वीय त्वरण) के मान में कमी आती है।

यह भी जाने-

प्रकाश का प्रकीर्णन किसे कहते है?, परिभाषा, उदाहरण, लार्ड रैले का प्रकीर्णन नियम समझे

उत्तल और अवतल दर्पण के उपयोग, अंतर, पहचान

प्रकाश का अपवर्तन किसे कहते है?, अपवर्तन के नियम, स्नैल का नियम, क्रान्तिक कोण तथा पूर्ण आन्तरिक परावर्तन उदाहरण सहित समझे

More Physics Concept- Click Here

Join us Now-

• WhatsApp
• Telegram
• Instagram

चन्द्रमा पर गुरुत्वीय त्वरण

चन्द्रमा पर पृथ्वी की तुलना में गुरुत्वीय त्वरण का मान 1/6 होता है। पृथ्वी पर गुरुत्वीय त्वरण 9.81 मीटर/सेकंड² होता है। अतः चन्द्रमा पर गुरुत्वीय त्वरण पृथ्वी से तुलना करने पर 9.81/6= 1.63 मीटर/सेकंड² होता है।

• चन्द्रमा का द्रव्यमान पृथ्वी के द्रव्यमान का 1/81 गुना होता है।
• चन्द्रमा की त्रिज्या पृथ्वी की त्रिज्या की 1/3.7 गुना होती है।

• Mm= चन्द्रमा का द्रव्यमान
• Rm= चन्द्रमा की त्रिज्या
• gm= चन्द्रमा पर गुरुत्वीय त्वरण

चन्द्रमा पर g का मान निकालने के लिए सूत्र=
$$g_m=\frac{G\;M_{m\;}}{R_m^2}$$
$$M_m=\frac{M_e}{81}\;and\;R_m=\frac{R_e}{3.7}$$

• Me= पृथ्वी का द्रव्यमान
• Re= पृथ्वी की त्रिज्या
• ge= पृथ्वी पर गुरुत्वीय त्वरण

यह मान सूत्र में रखने पर-

$$g_m=\frac{G\;M_e}{81\;\left({\displaystyle\frac{R_e}{3.7}}\right)^2}$$
$$g_m=\frac{G\;M_{e\;\;}\;\;\left(3.7\right)^2}{\left(R_e\right)^2\;\;\;\;81}$$
$$g_m=\frac{ge\;\left(3.7\right)^2}{81}$$
$$g_m=\frac{9.81\;\times\;\left(3.7\right)^2}{81}$$
$$g_m=1.658\;meter/second^2$$

अतः चन्द्रमा पर गुरुत्वीय त्वरण 1.658 मीटर/सेकंड² होता है।

video के माध्यम से समझने के लिए-

FAQ (Frequently Asked Questions)

Latest Posts-

• 
  न्यूटन का पहला नियम: परिभाषा, कारण, अनुप्रयोग, उदाहरण | जड़त्व का नियम, प्रकार
• 
  सार्थक अंक किसे कहते हैं, परिभाषा, उदाहरण, नियम, निकालने का तरीका | Significant figures in hindi
• 
  अभिकेंद्र त्वरण किसे कहते है?, परिभाषा, सूत्र, अभिकेंद्र त्वरण के सूत्र का निगमन, मात्रक, विमा जानें
• 
  कोटिमान किसे कहते है?, कोटिमान की परिभाषा, उदाहरण, कोटिमान ज्ञात करने का तरीका
• 
  निकट दृष्टि दोष तथा दूर दृष्टि दोष किसे कहते है? परिभाषा, कारण, निवारण को चित्र सहित समझे
• 
  वृत्तीय गति किसे कहते है? वृत्तीय गति के उदाहरण, परिभाषा, सूत्र, कोणीय विस्थापन, कोणीय वेग तथा रेखीय वेग में सम्बन्ध
• 
  पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन | Gravitational Acceleration below the Earth Surface
• 
  पृथ्वी तल से ऊपर जाने में g के मान में परिवर्तन | Gravitational Acceleration above the Earth Surface
• 
  सुनामी क्या है?, सुनामी कैसे आती है, परिभाषा, कारण, प्रभाव, सुनामी आपदा प्रबंधन, 2004 सुनामी चेतावनी प्रणाली
• 
  Derivation of the Formula for the rise of Liquid in a capillary Tube | केशनली में द्रव के उन्नयन के सूत्र का निगमन
• 
  केशिकत्व (capillarity) किसे कहते है, केशिकत्व की परिभाषा, उदाहरण, सूत्र, Practical Experiment
• 
  प्राथमिक रंग, द्वितीयक रंग तथा पूरक रंग किसे कहते है? चित्र व उदाहरण सहित जाने
• 
  आपदा किसे कहते हैं, परिभाषा, प्रकार, कारण, प्राकृतिक आपदा तथा मानवकृत आपदा क्या है?
• 
  प्रतिबल (Stress) किसे कहते है? परिभाषा, सूत्र, मात्रक, प्रतिबल के प्रकार, तनाव तथा संपीडन प्रतिबल, सीधे तथा नमन प्रतिबल, कर्तन तथा स्पर्शीय प्रतिबल किसे कहते है उदाहरण सहित जाने