पृथ्वी तल पर g (गुरुत्वीय त्वरण) का मान 9.81 मीटर/सेकंड² होता है। पृथ्वी तल से नीचे जाने पर g का मान लगातार घटता जाता है और पृथ्वी के केंद्र पर g का मान शून्य हो जाता है।
पृथ्वी तल से नीचे जाने में g का मान क्यों घटता है? तथा पृथ्वी के केंद्र में g का मान क्यों शून्य हो जाता है। इन सभी सवालों के जवाब, कारण, सूत्र, संबंध हम सरल भाषा में समझेंगे। इसके साथ पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन का सूत्र का निगमन करेंगे।
पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन का सूत्र
$$g’=g\left(1-\frac h{R_e}\right)$$
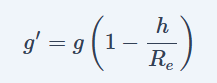
यहाँ,
- g’= गहराई में जाने पर परिवर्तित गुरुत्वीय त्वरण
- g = पृथ्वी तल पर गुरुत्वीय त्वरण
- h = पृथ्वी के तल से वस्तु की गहराई
- Re= पृथ्वी की त्रिज्या
समझने के लिए: हम एक वस्तु को पृथ्वी तल से h गहराई में ले गए है। नीचे गए स्थान पर हम वस्तु का परिवर्तित गुरुत्वीय त्वरण (g’) ऊपर दिए सूत्र की सहायता से ज्ञात कर सकते है। पृथ्वी तल पर g (गुरुत्वीय त्वरण) का मान 9.81 मीटर/सेकंड² होता है।
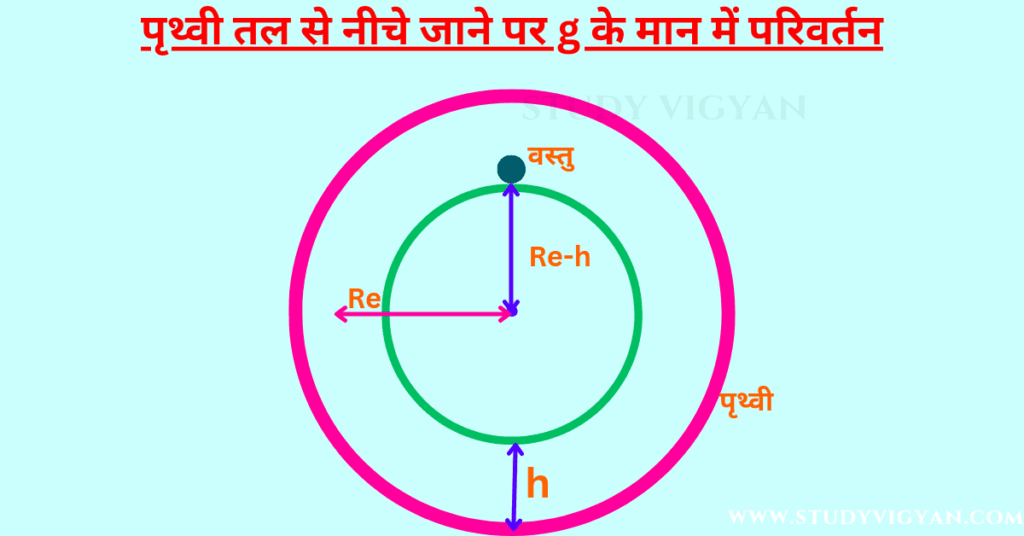
पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन सूत्र का निगमन (सम्बन्ध)
पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन सूत्र का निगमन (सम्बन्ध) करने से पहले हमें कुछ बातों का पता होना जरुरी है। जैसे-
- O = पृथ्वी का केंद्र
- Me = पृथ्वी का द्रव्यमान
- m = वस्तु का द्रव्यमान
- g’= पृथ्वी तल के नीचे जाने पर परिवर्तित गुरुत्वीय त्वरण
- g = पृथ्वी तल पर गुरुत्वीय त्वरण
- h = पृथ्वी से तल से वस्तु की गहराई
- Re= पृथ्वी की त्रिज्या
पृथ्वी की त्रिज्या Re है। वस्तु पृथ्वी से h गहराई में स्थित है। अतः वस्तु पृथ्वी के केंद्र से (Re-h) दूरी पर स्थित है। Re-h दूरी को त्रिज्या, O को केंद्र मानकर एक गोला खींचा जाता है।
(Re-h) त्रिज्या मानकर खींचे गए गोले का द्रव्यमान (M’)= आयतन × घनत्व
$$M’=\frac43\mathrm\pi\;{({\mathrm R}_{\mathrm e}-\mathrm h)}^3\;\times\;\mathrm\rho$$
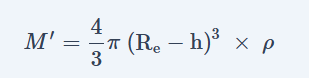
वस्तु (P) भीतर वाले गोले (Re-h त्रिज्या वाले) के तल पर स्थित है तथा यह बाहरी गोले (Re त्रिज्या वाले) के अंदर स्थित है। हम जानते है कि- किसी भी खोखले गोले के भीतर स्थित वस्तु पर आकर्षण बल शून्य होता है। अतः वस्तु (P) पर केवल भीतर वाले गोले के कारण आकर्षण बल कार्य करता है।
न्यूटन के नियमानुसार भीतर वाले गोले के कारण लगने वाला आकर्षण बल (F)=
$$F=\;\frac{G\;M’\;m}{{(R_e-h)}^2}=\;G\frac{{\displaystyle\frac43}\mathrm\pi{({\mathrm R}_{\mathrm e}-\mathrm h)}^3\;\mathrm\rho\;\mathrm m}{{(R_e-h)}^2}$$
$$F=\frac43\mathrm\pi{\;G\;({\mathrm R}_{\mathrm e}-\mathrm h)}\;\mathrm\rho\;\mathrm m\;$$
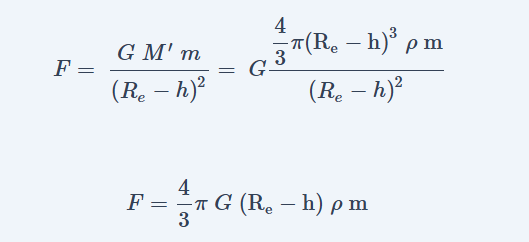
यह बल (F) पिण्ड के भार mg’ के बराबर होगा। (g’ पृथ्वी तल से h गहराई पर गुरुत्वीय त्वरण है।)
$$m\;g’=\frac43\mathrm\pi{\;G\;({\mathrm R}_{\mathrm e}-\mathrm h)}\;\mathrm\rho\;\mathrm m\;\;..\mathrm{equation}\;(1)$$
यदि कोई पिण्ड पृथ्वी तल पर हो जहाँ गुरुत्वीय त्वरण g है तो $$m\;g=\frac43\mathrm\pi{\;G\;{\mathrm R}_{\mathrm e}}\;\mathrm\rho\;\mathrm m\;\;……\mathrm{equation}\;(2)$$
समीकरण (1) को समीकरण (2) से भाग देने पर
(Equation 1 को Equation 2 से divide करने पर)
$$\frac{g’}g=\;\frac{R_e-h}{R_e}$$
$$\boldsymbol g\boldsymbol’\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol g\boldsymbol\;\mathbf{\left({1-\frac h{R_e}}\right)}$$
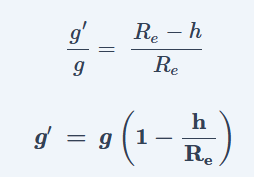
यही समीकरण पृथ्वी तल से नीचे जाने में g के मान में परिवर्तन का सूत्र (सम्बन्ध) है।
इस समीकरण से हम यह देख सकते है कि जैसे-जैसे h का मान बढ़ेगा उसे 1 से घटाने पर मान और अधिक कम हो जायेगा। जिसके कारण g’ का मान अधिक कम हो जायेगा।
g'<g
अतः समीकरण से भी सिद्ध होता है कि पृथ्वी तल से गहराई बढ़ने पर गुरुत्वीय त्वरण का मान कम होता है।
इससे यह सिद्ध होता है कि पृथ्वी तल से गहराई पर जाने में g (गुरुत्वीय त्वरण) के मान में कमी आती है।
गुरुत्वीय त्वरण का मात्रक मीटर/सेकण्ड2 होता है।
पृथ्वी के केन्द्र में g (गुरुत्वीय त्वरण) का मान
पृथ्वी के केन्द्र में g का मान शून्य होता है। पृथ्वी तल से नीचे जाने में h का मान लगातार घटता जाता है। एक समय यह मान Re के बराबर हो जाता है। गहराई h के Re के बराबर होने पर ऊपर-नीचे Re कट जायेगा और 1 आएगा। इस 1 को 1 से घटाने पर शून्य आएगा अतः यह सिद्ध होता है कि पृथ्वी के केन्द्र में g का मान शून्य होता है।
$$g’\;=\;g\;\left(1-\frac h{R_e}\right)$$
$$g’\;=\;g\;\left(1-\frac{R_{e\;}}{R_e}\right)$$
$$g’\;=\;g\;\left(1-\frac{1_\;}1\right)$$
$$g’\;=\;g\;\left(0\right)$$
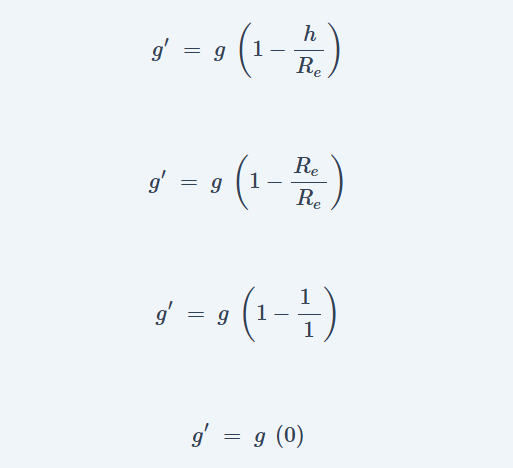
$$\boldsymbol g\boldsymbol’\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf0$$
अतः पृथ्वी के केन्द्र में g (गुरुत्वीय त्वरण) का मान शून्य होता है।
यह भी जाने-
विषुवत रेखा तथा ध्रुवों पर g का मान
विषुवत रेखा पर g का मान सबसे कम तथा ध्रुवों पर g का मान सबसे अधिक होता है। इसके दो कारण है-
- पृथ्वी की आकृति
- पृथ्वी का अपनी अक्ष के परितः घूमना
पृथ्वी की आकृति: पृथ्वी पूरी तरह गोल नहीं है। पृथ्वी का आकार अण्डाकार है। यह दोनों ध्रुवों पर कुछ चपटी है। चपटा होने के कारण पृथ्वी के उत्तरी और दक्षिणी ध्रुवों के बीच की त्रिज्या विषुवत रेखीय त्रिज्या से 21 किलोमीटर कम होती है। हम जानते है कि गुरुत्वाकर्षण बल पृथ्वी की त्रिज्या पर निर्भर करता है। गुरुत्वीय त्वरण (Gravitational Acceleration)=
$$g=\frac{G\;M_e}{R_e^2}$$
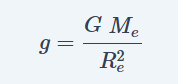
- G= सार्वत्रिक गुरुत्वाकर्षण नियतांक
- Me= पृथ्वी का द्रव्यमान
- Re= पृथ्वी की त्रिज्या
G और Me का मान नियत रहता है। अतः सूत्र में हम देख सकते है कि पृथ्वी की त्रिज्या (Re) बढ़ने पर g का मान कम होता है। पृथ्वी की त्रिज्या (Re) कम होने पर g का मान बढ़ता है।
पृथ्वी का अपनी अक्ष के परितः घूमना: पृथ्वी अपने अक्ष के चारों ओर घूमती है। जिसके कारण पृथ्वी तल पर स्थित प्रत्येक वस्तु भी वृत्तीय पथ पर घूम रही है। वृत्तीय पथ पर घूमने वाली वस्तु में वृत्त के केन्द्र की ओर एक अभिकेंद्रीय त्वरण कार्य करता है।
यह अभिकेंद्रीय त्वरण, गुरुत्वीय त्वरण से ही उत्पन्न होती है। इसका मतलब यह है कि पृथ्वी के गुरुत्वीय त्वरण का मान उस मान से कम होता है जो कि पृथ्वी की अक्षीय घूर्णन गति की अनुपस्थिति में पृथ्वी तल के प्रत्येक बिंदु पर होता। g के मान में यह कमी अलग-अलग स्थानों पर अलग-अलग होती है। इसी कारण पृथ्वी तल पर g का मान अक्षांश के साथ बदलता रहता है।
Join us Now
पृथ्वी तल के नीचे जाने पर g का मान में परिवर्तन – Watch Video
FAQ (Frequently Asked Questions)
पृथ्वी तल से नीचे जाने पर गुरुत्वीय त्वरण (g) का मान क्या होता है?
पृथ्वी तल से नीचे जाने पर g का मान घटता जाता है। पृथ्वी तल पर g का मान 9.81 मीटर/सेकंड² होता है। जैसे-जैसे हम पृथ्वी तल से नीचे जाते है g का मान घटता जाता है और पृथ्वी के केन्द्र में गुरुत्वीय त्वरण का मान शून्य हो जाता है। लेख में सूत्र तथा समीकरणों की सहायता से बेहतरीन ढंग से समझाया गया है।
पृथ्वी की ऊंचाई और गहराई का g के मान पर क्या प्रभाव पड़ता है?
पृथ्वी में ऊंचाई तथा गहराई दोनों बढ़ने पर g के मान में कमी आती है।
पृथ्वी पर 0 गुरुत्वाकर्षण कहाँ है?
पृथ्वी तल के नीचे जाने पर g का मान घटता है और पृथ्वी के केंद्र में 0 गुरुत्वाकर्षण होता है।
पृथ्वी पर गुरुत्वाकर्षण सबसे न्यूनतम कहां है?
पृथ्वी तल पर g का मान सबसे कम विषुवत रेखा पर होता है। तथा पृथ्वी के केंद्र में शून्य होता है।
Latest Posts-
- इंजीनियरिंग ड्राइंग में रेखाएं कितने प्रकार की होती है?, इंजीनियरिंग ड्राइंग में रेखा किसे कहते है?, विभिन्न रेखाओं के उपयोग, विशेषता, मोटाई, उदाहरण चित्र सहित जानें
- Ibps rrb po mains result 2024 कैसे चेक करें? इंटरव्यू कितने अंक का होता है? महत्वपूर्ण जानकारी
- इंजीनियरिंग ड्राइंग में टाइटल ब्लॉक को कैसे बनाते हैं?, टाइटल ब्लॉक का डिज़ाइन, आकार, प्रकार, परिभाषा, 8 जरुरी सावधानियों को जानें
- न्यूटन का पहला नियम (Newton’s First Law): परिभाषा, कारण, अनुप्रयोग, उदाहरण | जड़त्व का नियम (Law of Inertia), प्रकार
- विकृति ऊर्जा (Strain Energy) की परिभाषा, सूत्र, निगमन, मात्रक और ऊर्जा गुणांक को चित्र सहित जानें | प्रमाण विकृति ऊर्जा, प्रमाण प्रतिबल, विकृति क्या होते है?
- गुणोत्तर श्रेणी (Geometric Progression): परिभाषा, गुणोत्तर श्रेणी के सूत्र, योग, सवाल व गुणोत्तर माध्य को उदाहरण सहित
- केशिकत्व (Capillarity): परिभाषा, सिद्धांत, उदाहरण, सूत्र और प्रैक्टिकल
- जल में पड़े सिक्के या वस्तु का कुछ उठा हुआ प्रतीत होना
- आपदा: परिभाषा, प्रकार, उदाहरण, प्रभाव | प्राकृतिक और मानवकृत आपदा के कारण
- प्रकाश का अपवर्तन (Refraction of Light): अर्थ, परिभाषा, अपवर्तन के नियम, स्नैल का नियम, सूत्र तथा क्रान्तिक कोण तथा पूर्ण आन्तरिक परावर्तन को उदाहरण सहित समझे
- समांतर श्रेणी (Arithmetic Progression) किसे कहते हैं, इसकी परिभाषा, समांतर श्रेणी के सूत्र, योग, सवाल व समांतर माध्य को उदाहरण सहित जानें
- कोटिमान (Order of Magnitude): कोटिमान किसे कहते है?, परिभाषा, उदाहरण, कोटिमान ज्ञात करने का तरीका सीखें
- सार्थक अंक (Significant figures): परिभाषा, उदाहरण, नियम, सार्थक अंक निकालने का तरीका
- पूर्ण आंतरिक परिवर्तन के उदाहरण: रेगिस्तान में मरीचिका का बनना, हीरे का चमकना, जल में परखनली का चमकना
- अवतल दर्पण में वस्तु की स्थिति एवं प्रतिबिंब का बनना और उत्तल दर्पण में वस्तु की स्थिति और प्रतिबिम्ब का बनना
- प्रकाश का प्रकीर्णन क्या है? इसकी परिभाषा को उदाहरण सहित जानें, लार्ड रैले का प्रकीर्णन नियम सिद्ध सहित समझे
- 1000 वर्ग फीट ढलाई करने में सामान की मात्रा और कीमत
- शेषफल कैसे निकालते हैं? | Sheshfal kaise nikale
- How to find last two digits of a number in hindi, Best tricks | संख्या के अंतिम दो अंक ज्ञात करना सीखें
- इकाई अंक किसे कहते हैं | इकाई अंक ज्ञात करना | इकाई अंक के सवाल | Unit Digit in hindi
